As I waited for my SAS code for practicum to run, I came across a Super Bowl commercial by the NFL, shown below. The commercial starts with the claim that “9 months after a Super Bowl victory, winning cities see a rise in births.” While it is humorous and easy to imagine why this may occur, I wanted to see if there is any truth to the claim.
Unfortunately, the NFL did not provide the data it used to make the claim,
so I had to find data on my own.
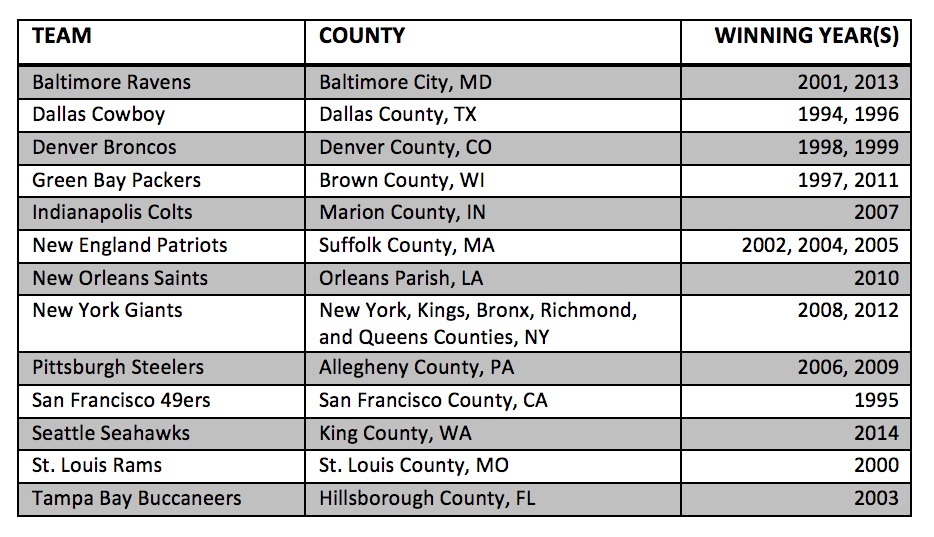
The National Vital Statistics System, under the Center for Disease Control and Prevention, has county and monthly level birth data from 1990-2014 for public use. Since the data is at a county level, I found the county that best matched the location of the team, shown below. I only looked at November births, which is 9 months after the Super Bowl, and studied 21 Super Bowl winners from 1994-2014.
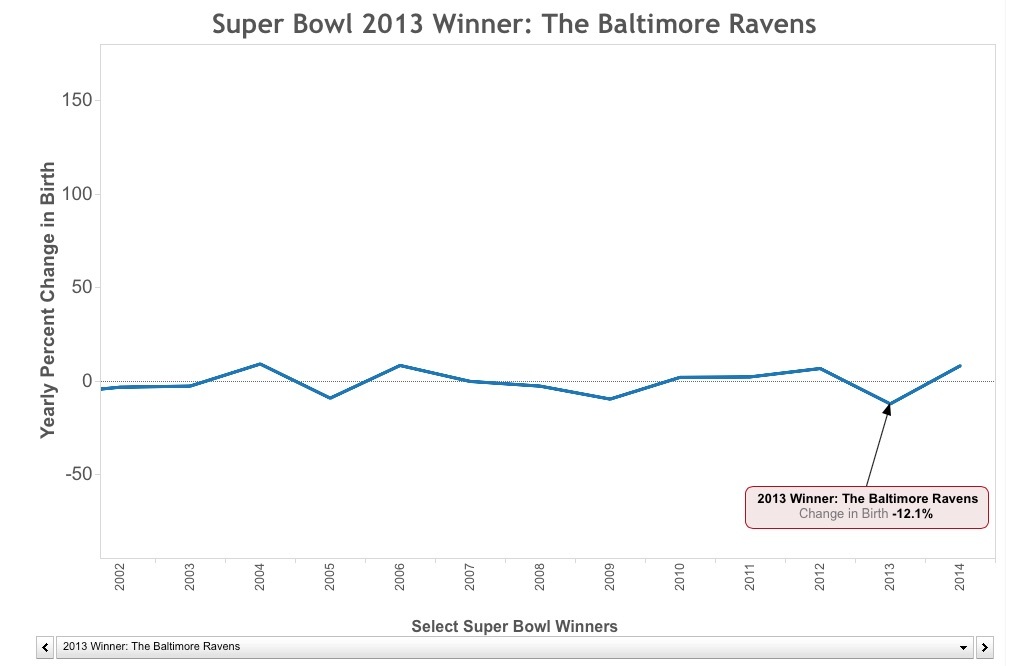
To see if the Super Bowl has an effect on the birth rates in that county, I compared the change in births from the previous year. For example, the Baltimore Ravens won the Super Bowl in 2013, I found the percent change in births when November births in 2013 are compared to 2012. If the Super Bowl had an effect, then there should be more births in 2013 than in 2012 in Baltimore. Below is how the percent change in birth differs for all Super Bowl winning counties from 1994-2014.
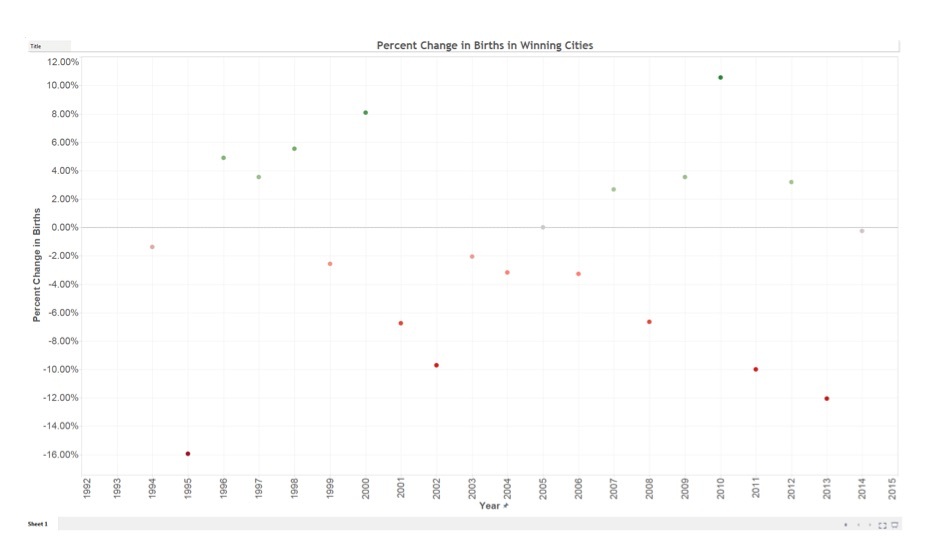
Overall, there are eight occasions where there were more births in the Super Bowl winning year than its previous year, and twelve occasions where there are fewer births. There was also one occasion with no change, which surprisingly happened when the New England Patriots won two Super Bowls in a row. For the most part, the percent change in birth for the Super Bowl winning county is random in this study.
Finally, it is important to note that there are several factors that could affect births in an area. However, since the NFL did not provide the source of their data, they could have found evidence to support their claim. However, even if they did find correlations, it is important to remember a fundamental rule of statistics: Correlation Does Not Imply Causation.
Columnist: Ashutosh Garg

